Skip to main content

Math 1

Algebra

23=8; 33=9; 43=64; 53=125; 63=216; 73=343; 83=512; 93=729; 103=1000
  1. (a+b)2=a2+2ab+b2
  2. (a-b)2=a2-2ab+b2 
  3. (a+b)2=(a-b)2+4ab 
  4. (a-b)2=(a+b)2-4ab
  5.   a2+b2=(a-b)2+2ab
  6. a2+b2=(a+b)2-2ab
  7.  a2-b2=(a+b)(a-b)
  8.  2(a2+b2)=(a+b)2+(a-b)2
  9. ab=((a+b)/2)2-((a-b)/2)2
  10. (a+b)3=a3+3a2b+3ab2+b3
  11. (a-b)3=a3-3ab2+3ab2-b3
  12. (a+b)3=a3+b3+3ab(a+b)
  13. (a-b)3=a3-b3-3ab(a-b)
  14. a3+b3=(a+b)3-3ab(a+b)
  15. a3+b3=(a+b)(a2-ab+b2)
  16. a3-b3=(a-b)3+3ab(a-b)
  17. a3-b3=(a-b)(a2+ab+b2)
  18. (a+b+c)2=a2+b2+c2+2(ab+bc+ca)
  19. a2+b2+c2=(a+b+c)2-2(ab+bc+ca)
  20. ab+bc+ca=((a+b+c)2-(a2+b2+c2))/2
  21. 4ab=(a+b)2-(a-b)2

Measurement


litre,
Milli,centi,deci, metre,deca,hecto,kilo
gram,
Multiply by 10 in each step<=||=>divided by 10 in each step

Basic Trigonometry

1c(radian)=(2x900)/π, cse=cosec

  1. sinϴ=opposite/hypotenuse
  2. cosϴ=adjacent/hypotenuse
  3. tanϴ=opposite/adjacent
  4. cotϴ=adjacent/opposite
  5. cosecϴ=hypotenuse/opposite
  6. secθ=hypotenuse/adjacent
  7. sinθ/cosθ=tanθ
  8. secθ/cosecθ=tanθ
  9. cosθ/sinθ=cotθ
  10. cosecθ/secθ=cotθ
  11. sinθ=1/cosecθ
  12. cosθ=1/secθ
  13. tanθ=1/cotθ
  14. cotθ=1/tanθ
  15. cosecθ=1/sinθ
  16. secθ=1/cosθ
  17.  sin2ϴ+cos2ϴ=1
  18. sec2ϴ-tan2ϴ=1
  19. cosec2ϴ-cot2ϴ=1
  20.   sin(900-ϴ)=cosϴ
  21.     cos(900-ϴ)=sinϴ
  22.     tan(900-ϴ)=cotϴ
  23.   cot(900-ϴ)=tanϴ
  24.   cosec(900-ϴ)=secϴ
  25.     sec(900-ϴ)=cosecϴ

Relation among Trigonometric Ratios


Trigonometrical Ratio in Complementary Angle









Simple interest

  1. Interest(I)=Ptr/100
  2. Rate of interest(r)=I100/(Pt)
  3. Principal(P)=I100/tr
  4. Time(t)=I100/Pr

Compound Interest including principal


  1. Compound Interest including principal(I)=P(1+r/100)t

Arithmetic

  1. dividend=(divider x quotient)+remainder
  2. L.C.M.=(first number x second number)/G.C.D.
  3. G.C.D.=(first number x second number)/L.C.M.
  4. first number=(L.C.M. x G.C.D.)/Second number
  5. Second  number=(L.C.M. x G.C.D.)/First number

2D Shapes




 Rectangle

  1. Range of rectangle=2x(Length+width)
  2. area of rectangle=Length x width
  3. width of rectangle=area/Length 
  4. length of rectangle=area/width
  5. diagonal of rectangle=√(Length2+width2) 

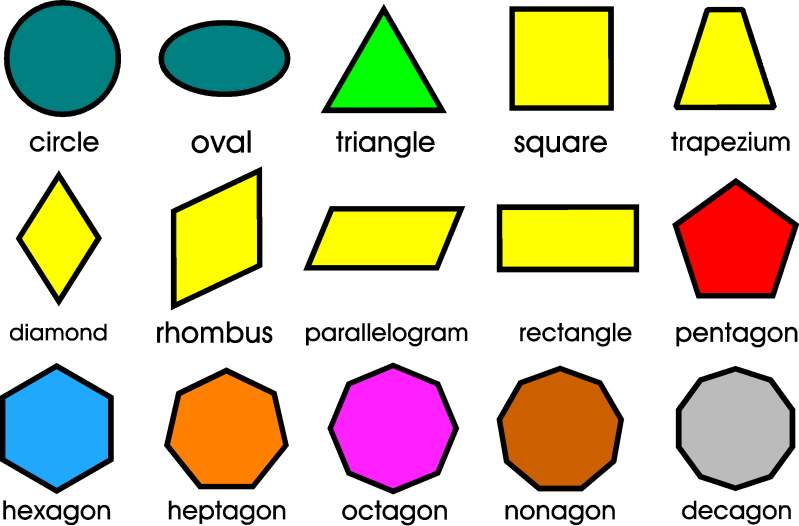
square

  1. range of square=4 x length of a side
  2. area of a square=side x side
  3. diagonal of a side=side x √2
  4. area of a square= 1/2 x diagonal2
  5. side of a square= range/4=√area

 triangle

  1. adjacent of triangle=2 x area/height
  2. area of a triangle=1/2 x adjacent x height
  3. height of a triangle=2 x area/adjacent
  4. area of a equilateral triangle=√3/4 x side2
  5. height of equilateral triangle=√3/2 x side
  6. height of isosceles triangle=√((square of any one side between equal sides)/(square of half of adjacent))
  7. area of a zodiacal triangle=  √(s(s-a)(s-b)(s-c))          [here s is semi range of that triangle; and a,b,c are lengths of three of three sides]

parallelogram,trapezium,rhombus 



  1. area of parallelogram=adjacent x height
  2. area of trapezium=1/2 x (summation of parallel sides x distance of 
  4. parallel sides)
  5. area of rhombus=1/2 x multiplication of diagonals

circle


π=pi

π=circumference/radius=22/7
circumference=π x diameter
diameter(d)=circumference/π
radius=circumference/(2π)
range of semi circular shape=πr+2r
area(A)=πr2
r=√(A/π)= √(7A/22 )
radius of inner circle of equilateral triangle=side/(2√3)
diameter of inner circle of equilateral triangle=side/√3

3D SHAPES

cuboid

Lateral surface area of cuboid = 2h(l+b)
total surface area= 2(lb+hl+hb)
volume=adjacent area x height

cube

total surface area of a cube =6 x side2
volume=side3
diagonal of a cube=√3 x side

Prism

Lateral surface area of Prism= Range of adjacent x height
total surface area = Lateral surface area + 2 x adjacent area
volume = adjacent area x height

Cylinder 

adjacent surface area= πr2
Lateral surface area of cylinder=circumference x height
total surface area= 2 x adjacent surface area + Lateral surface area
volume of tube=adjacent surface area x height

Hollow tube 

outer radius=r1  ,inner radius=r2  , height =h
 volume=π(r12 -r22 )h   
area of inner and outer curved face= 2π(r1+r2)h 

right pyramid

Lateral surface area of right pyramid= 1/2 x adjacent surface area  x height
total surface area of right pyramid=adjacent surface area + Lateral surface area
volume=1/3 x adjacent surface x height

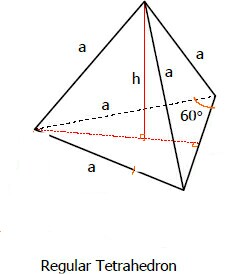
each surface of regular tetrahedron=√3/4 x a2
total surface of regular tetrahedron=4 x √3/4 x a2

cone

Lateral surface area of cone=πr x slant height=1/2 x adjacent circumference x slant height
total surface= adjacent area+Lateral surface area 
volume=1/3 x adjacent area x height
slant height=√(radius2+height2)

sphere

area of total surface=4πr2
volume=4/3πr3
area of total surface of solid semi sphere=3πr2
volume of solid semi sphere=2/3πr3

Labels:

Comments

Post a Comment