ax^{2}+bx+c=0.

x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.

x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0.

Subtract

c / a

from both sides of the equation, yielding:

x^{2}+{\frac {b}{a}}x=-{\frac {c}{a}}.

x^{2}+{\frac {b}{a}}x+\left({\frac {b}{2a}}\right)^{2}=-{\frac {c}{a}}+\left({\frac {b}{2a}}\right)^{2},

which produces:

\left(x+{\frac {b}{2a}}\right)^{2}=-{\frac {c}{a}}+{\frac {b^{2}}{4a^{2}}}.

Accordingly, after rearranging the terms on the right hand side to have a common denominator, we obtain:

\left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}.

x+{\frac {b}{2a}}=\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}.

Isolating

x

gives the quadratic formula:

x={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}.

x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\quad {\text{and}}\quad x={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}

x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}.

Other derivations

Many alternative derivations of the quadratic formula are in the literature. These derivations may be simpler than the standard completing the square method, may represent interesting applications of other algebraic techniques, or may offer insight into other areas of mathematics.

In other words, the quadratic formula can be derived as follows:

\begin{align} ax^2+bx+c &= 0 \\ 4 a^2 x^2 + 4abx + 4ac &= 0 \\ 4 a^2 x^2 + 4abx &= -4ac \\ 4 a^2 x^2 + 4abx + b^2 &= b^2 - 4ac \\ (2ax + b)^2 &= b^2 - 4ac \\ 2ax + b &= \pm \sqrt{b^2-4ac} \\ 2ax &= -b \pm \sqrt{b^2-4ac} \\ x &= \frac{-b\pm\sqrt{b^2-4ac }}{2a} \\ \end{align}

a(y+m)^{2}+b(y+m)+c=0.

Expanding the result and then collecting the powers of

y

produces:

ay^{2}+y(2am+b)+\left(am^{2}+bm+c\right)=0.

We have not yet imposed a second condition on

y

and

m

, so we now choose

m

so that the middle term vanishes. That is,

2 am + b = 0

or

m = - b / 2 a

. Subtracting the constant term from both sides of the equation (to move it to the right hand side) and then dividing by

a

gives:

y^{2}={\frac {-\left(am^{2}+bm+c\right)}{a}}.

Substituting for

m

gives:

y^{2}={\frac {-\left({\frac {b^{2}}{4a}}+{\frac {-b^{2}}{2a}}+c\right)}{a}}={\frac {b^{2}-4ac}{4a^{2}}}.

Therefore,

y=\pm {\frac {\sqrt {b^{2}-4ac}}{2a}};

substituting

x = y + m = y - b / 2 a

provides the quadratic formula.

By using algebraic identities

The following method was used by many historical mathematicians:

Let the roots of the standard quadratic equation be

r 1

and

r 2

. The derivation starts by recalling the identity:

(r_{1}-r_{2})^{2}=(r_{1}+r_{2})^{2}-4r_{1}r_{2}.

Taking the square root on both sides, we get:

r_{1}-r_{2}=\pm {\sqrt {(r_{1}+r_{2})^{2}-4r_{1}r_{2}}}.

Since the coefficient

a \neq 0

, we can divide the standard equation by

a

to obtain a quadratic polynomial having the same roots. Namely,

x^2 + \frac{b}{a}x + \frac{c}{a} = (x - r_1)(x-r_2) = x^2 - (r_1 + r_2)x + r_1 r_2.

From this we can see that the sum of the roots of the standard quadratic equation is given by

- b / a

, and the product of those roots is given by

c / a

. Hence the identity can be rewritten as:

r_{1}-r_{2}=\pm {\sqrt {\left(-{\frac {b}{a}}\right)^{2}-4{\frac {c}{a}}}}=\pm {\sqrt {{\frac {b^{2}}{a^{2}}}-{\frac {4ac}{a^{2}}}}}=\pm {\frac {\sqrt {b^{2}-4ac}}{a}}.

Now,

r_1 = \frac{(r_1 + r_2) + (r_1 - r_2)}{2} = \frac{-\frac{b}{a} \pm \frac{\sqrt{b^2 - 4ac}}{a}}{2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}.

Since

r 2 = - r 1 - b / a

, if we take

r_1 = \frac{-b + \sqrt{b^2 - 4ac}}{2a}

then we obtain

r_{2}={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}};

and if we instead take

r_1 = \frac{-b - \sqrt{b^2 - 4ac}}{2a}

then we calculate that

r_2 = \frac{-b + \sqrt{b^2 - 4ac}}{2a}.

Combining these results by using the standard shorthand ±, we have that the solutions of the quadratic equation are given by:

x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.

x^2+px+q,

assume that it factors as

x^2+px+q=(x-\alpha)(x-\beta),

Expanding yields

x^2+px+q=x^2-(\alpha+\beta)x+\alpha \beta,

where

p = -(α + β)

and

q = αβ

.

\begin{align} r_1 &= \alpha + \beta\\ r_2 &= \alpha - \beta. \end{align}

\begin{align} \alpha &= \textstyle{\frac{1}{2}}\left(r_1+r_2\right)\\ \beta &= \textstyle{\frac{1}{2}}\left(r_1-r_2\right). \end{align}

Thus, solving for the resolvents gives the original roots.

Now

r 1 = α + β

is a symmetric function in

α

and

β

, so it can be expressed in terms of

p

and

q

, and in fact

r 1 = - p

as noted above. But

r 2 = α - β

is not symmetric,

(\alpha - \beta)^2 = (\alpha + \beta)^2 - 4\alpha\beta\!

yields

r_2^2 = p^2 - 4q\!

and thus

r_2 = \pm \sqrt{p^2 - 4q}.\!

If one takes the positive root, breaking symmetry, one obtains:

\begin{align} r_1 &= -p\\ r_2 &= \sqrt{p^2 - 4q} \end{align}

and thus

{\begin{aligned}\alpha &={\tfrac {1}{2}}\left(-p+{\sqrt {p^{2}-4q}}\right)\\\beta &={\tfrac {1}{2}}\left(-p-{\sqrt {p^{2}-4q}}\right)\end{aligned}}

Thus the roots are

\textstyle{\frac{1}{2}}\left(-p \pm \sqrt{p^2 - 4q}\right)

which is the quadratic formula. Substituting

p = b / a, q = c / a

yields the usual form for when a quadratic is not monic. The resolvents can be recognized as

r 1 / 2 = - p / 2 = - b / 2 a

being the vertex, and

r 22 = p 2 - 4 q

is the discriminant (of a monic polynomial).

{\begin{aligned}a\left({\frac {-b}{2a}}+q\right)^{2}+b\left({\frac {-b}{2a}}+q\right)+c&=0\\[5pt]\left({\frac {-b}{2a}}+q\right)^{2}+{\frac {b}{a}}\left({\frac {-b}{2a}}+q\right)+{\frac {c}{a}}&=0&&(a\neq 0)\\[5pt]{\frac {b^{2}}{4a^{2}}}+q^{2}-{\frac {bq}{a}}-{\frac {b^{2}}{2a^{2}}}+{\frac {bq}{a}}+{\frac {c}{a}}&=0\\[5pt]{\frac {-b^{2}}{4a^{2}}}+q^{2}+{\frac {c}{a}}&=0\\[5pt]q^{2}&={\frac {b^{2}-4ac}{4a^{2}}}\\[5pt]q&={\frac {\pm {\sqrt {b^{2}-4ac}}}{2a}}\\[5pt]\end{aligned}}

The value of

x

in the extreme point is then added to both sides of the equation

x_{0}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}

Permutation

P(n,k)=\underbrace {n\cdot (n-1)\cdot (n-2)\cdots (n-k+1)} _{k\ \mathrm {factors} }

,

which is 0 when k > n, and otherwise is equal to

{\frac {n!}{(n-k)!}}.

Combination

,

C(n,k)={\frac {P(n,k)}{P(k,k)}}={\frac {\tfrac {n!}{(n-k)!}}{\tfrac {k!}{0!}}}={\frac {n!}{(n-k)!\,k!}}.

Binomial theorem

According to the theorem, it is possible to expand any power of x + y into a sum of the form

(x+y)^{n}={n \choose 0}x^{n}y^{0}+{n \choose 1}x^{n-1}y^{1}+{n \choose 2}x^{n-2}y^{2}+\cdots +{n \choose n-1}x^{1}y^{n-1}+{n \choose n}x^{0}y^{n},

(x+y)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}y^{k}=\sum _{k=0}^{n}{n \choose k}x^{k}y^{n-k}.

(1+x)^{n}={n \choose 0}x^{0}+{n \choose 1}x^{1}+{n \choose 2}x^{2}+\cdots +{n \choose {n-1}}x^{n-1}+{n \choose n}x^{n},

or equivalently

(1+x)^{n}=\sum _{k=0}^{n}{n \choose k}x^{k}.

Examples

Pascal's triangle

The most basic example of the binomial theorem is the formula for the square of

x + y

:

(x+y)^{2}=x^{2}+2xy+y^{2}.

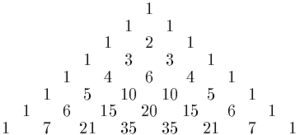
The binomial coefficients 1, 2, 1 appearing in this expansion correspond to the second row of Pascal's triangle. (Note that the top "1" of the triangle is considered to be row 0, by convention.) The coefficients of higher powers of

x + y

correspond to lower rows of the triangle:

{\begin{aligned}\\[8pt](x+y)^{3}&=x^{3}+3x^{2}y+3xy^{2}+y^{3},\\[8pt](x+y)^{4}&=x^{4}+4x^{3}y+6x^{2}y^{2}+4xy^{3}+y^{4},\\[8pt](x+y)^{5}&=x^{5}+5x^{4}y+10x^{3}y^{2}+10x^{2}y^{3}+5xy^{4}+y^{5},\\[8pt](x+y)^{6}&=x^{6}+6x^{5}y+15x^{4}y^{2}+20x^{3}y^{3}+15x^{2}y^{4}+6xy^{5}+y^{6},\\[8pt](x+y)^{7}&=x^{7}+7x^{6}y+21x^{5}y^{2}+35x^{4}y^{3}+35x^{3}y^{4}+21x^{2}y^{5}+7xy^{6}+y^{7}.\end{aligned}}

{n \choose k}={\frac {n!}{k!(n-k)!}}

which is defined in terms of the factorial function n!. Equivalently, this formula can be written

{n \choose k}={\frac {n(n-1)\cdots (n-k+1)}{k(k-1)\cdots 1}}=\prod _{\ell =1}^{k}{\frac {n-\ell +1}{\ell }}=\prod _{\ell =0}^{k-1}{\frac {n-\ell }{k-\ell }}

Inductive proof

(x+y)^{n+1}=x(x+y)^{n}+y(x+y)^{n}

shows that (x + y)^{n + 1} also is a polynomial in x and y, and

[(x+y)^{n+1}]_{j,k}=[(x+y)^{n}]_{j-1,k}+[(x+y)^{n}]_{j,k-1},

since if j + k = n + 1, then (j − 1) + k = n and j + (k − 1) = n. Now, the right hand side is

{\binom {n}{k}}+{\binom {n}{k-1}}={\binom {n+1}{k}},

(x+y)^{n+1}=\sum _{k=0}^{n+1}{\tbinom {n+1}{k}}x^{n+1-k}y^{k},

which is the inductive hypothesis with n + 1 substituted for n and so completes the inductive step.

Generalizations

Newton's generalized binomial theorem

{r \choose k}={\frac {r\,(r-1)\cdots (r-k+1)}{k!}}={\frac {(r)_{k}}{k!}},

{\begin{aligned}(x+y)^{r}&=\sum _{k=0}^{\infty }{r \choose k}x^{r-k}y^{k}\\&=x^{r}+rx^{r-1}y+{\frac {r(r-1)}{2!}}x^{r-2}y^{2}+{\frac {r(r-1)(r-2)}{3!}}x^{r-3}y^{3}+\cdots .\end{aligned}}

When r is a nonnegative integer, the binomial coefficients for k > r are zero, so this equation reduces to the usual binomial theorem, and there are at most r + 1 nonzero terms. For other values of r, the series typically has infinitely many nonzero terms.

For example, with r = 1/2 gives the following series for the square root:

{\sqrt {1+x}}=\textstyle 1+{\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+{\frac {7}{256}}x^{5}-\cdots

(1+x)^{-1}={\frac {1}{1+x}}=1-x+x^{2}-x^{3}+x^{4}-x^{5}+\cdots

More generally, with r = −s:

{\frac {1}{(1-x)^{s}}}=\sum _{k=0}^{\infty }{s+k-1 \choose k}x^{k}\equiv \sum _{k=0}^{\infty }{s+k-1 \choose s-1}x^{k}.

So, for instance, when

s=1/2

,

{\frac {1}{\sqrt {1+x}}}=\textstyle 1-{\frac {1}{2}}x+{\frac {3}{8}}x^{2}-{\frac {5}{16}}x^{3}+{\frac {35}{128}}x^{4}-{\frac {63}{256}}x^{5}+\cdots

Multinomial theorem

The binomial theorem can be generalized to include powers of sums with more than two terms. The general version is

(x_{1}+x_{2}+\cdots +x_{m})^{n}=\sum _{k_{1}+k_{2}+\cdots +k_{m}=n}{n \choose k_{1},k_{2},\ldots ,k_{m}}x_{1}^{k_{1}}x_{2}^{k_{2}}\cdots x_{m}^{k_{m}}.

where the summation is taken over all sequences of nonnegative integer indices k₁ through k_m such that the sum of all k_i is n. (For each term in the expansion, the exponents must add up to n). The coefficients

{\tbinom {n}{k_{1},\cdots ,k_{m}}}

are known as multinomial coefficients, and can be computed by the formula

{n \choose k_{1},k_{2},\ldots ,k_{m}}={\frac {n!}{k_{1}!\cdot k_{2}!\cdots k_{m}!}}.

Combinatorially, the multinomial coefficient

{\tbinom {n}{k_{1},\cdots ,k_{m}}}

counts the number of different ways to partition an n-element set into disjoint subsets of sizes k₁, ..., k_m.

Multi-binomial theorem

It is often useful when working in more dimensions, to deal with products of binomial expressions. By the binomial theorem this is equal to

(x_{1}+y_{1})^{n_{1}}\dotsm (x_{d}+y_{d})^{n_{d}}=\sum _{k_{1}=0}^{n_{1}}\dotsm \sum _{k_{d}=0}^{n_{d}}{\binom {n_{1}}{k_{1}}}\,x_{1}^{k_{1}}y_{1}^{n_{1}-k_{1}}\;\dotsc \;{\binom {n_{d}}{k_{d}}}\,x_{d}^{k_{d}}y_{d}^{n_{d}-k_{d}}.

This may be written more concisely, by multi-index notation, as

(x+y)^{\alpha }=\sum _{\nu \leq \alpha }{\binom {\alpha }{\nu }}x^{\nu }y^{\alpha -\nu }.

\cos \left(nx\right)+i\sin \left(nx\right)=\left(\cos x+i\sin x\right)^{n}.

Using the binomial theorem, the expression on the right can be expanded, and then the real and imaginary parts can be taken to yield formulas for cos(nx) and sin(nx). For example, since